土壤质量综合评价与土壤中各种元素的含量有着密切的联系。重金属元素含量对土壤污染程度具有决定性影响，反映土壤肥力状况的OM、TN、AP、AK和土壤盐分等特征与土壤中的Ca、Cu、Fe、Zn、Mn息息相关。因此，一种有效的土壤元素含量测量方法对于判定土壤质量、合理利用土壤资源等具有重要意义。

土壤中元素含量的常规测量分析方法主要有分光光度法、电感耦合等离子体原子发射光谱法和原子吸收光谱法等，这些方法都已比较成熟，其特点时精度高、结果可靠，但是也存在很大的问题和不便，其对样本的前处理过程十分繁琐，并且在处理过程中需要使用到大量的化学处理方法，容易造成对环境的二次污染。X射线荧光光谱检测技术(XRF)是一种元素含量分析技术，XRF因其成本低、速度快、元素范围广等优势成为了土壤元素含量分析的主要方法之一，且目前已广泛应用于物理、化学、生物、环境、工业生产等领域。

在基于XRF的元素定量分析中，理论上讲，土壤中元素的含量计算主要通过测量元素对应的特征峰强度建立校准曲线进行，如通过偏最小二乘法（PLS）或使用常规的数学分析方法处理谱线强度与元素含量的拟合分析。然而，XRF测量时元素间基体效应、光电吸收增强效应、数据自身的本底噪声等使得元素含量的测量是一个非线性过程，难以准确预测。然而，单变量线性校准方法PLS，可能难以适当拟合分析信号和所研究参数之间的非线性关系，不能取得很好的结果。在这种情况下，一些非线性校准方法，如支持向量机回归(support vector machine,SVR)、Back Propagation(BP)、Adaboost等算法可以提供更好的模型调整能力和预测结果。此外，在XRF定量分析中，一般无法获取大量且全面的标定样本进行测量，使得很多基于统计的神经网络方法也很难取得很好的效果。而SVR算法作为一种多元非线性的回归算法，SVR具有很高的泛化性能，即使使用小样本集也能提供良好的模型。

本文研究了XRF技术结合SVR算法定量分析土壤中各元素含量的可行性。首先，基于贝叶斯全局优化算法(BOA)对SVR模型优化，解决SVR对超参数的敏感性和依赖性问题。然后针对XRF光谱数据，采用迭代离散小波变换(IDWT)对样本进行预处理，然后计算样本中各元素的组分信息作为模型输入提高预测精度。同时，本文研究了不同的输入特征对性能的影响并提出了基于灵敏度分析的特征降维方法，基于最优的输入变量和模型参数构建定量分析模型，最后将模型应用于土壤元素的定量分析，并与单参数PLS算法进行了比较。

2.1土壤样品采集和XRF光谱采集

本实验使用的设备是由使用泰克鑫科(TECSYNC)公司生产的手持式ED-XRE光谱仪进行测量，型号为TS-XH4000-SOIL，该设备的X射线管在45KV和25uA下正常工作。实验中采用了55个国标样品作为土壤标准样品。

图1 光谱仪数据采集过程

2.2基于灵敏度分析的特征降维方法

在XRF元素含量定量分析中，元素间基体效应、仪器自身噪音等会导致一个元素的组分信息往往受到其它元素和仪器的干扰。其中谱线干扰是定量分析中的主要误差源之一，当元素的特征x射线波长几乎相等时，x射线强度测量将受到干扰。元素的定量分析主要受重叠峰和逃逸峰的影响。同时，对于SVR，由太多的变量会不利于建模，严重的变量间共线关系会影响模型的准确性和稳定性。因此，为了进一步提高模型的定量分析能力，有必要去除XRF光谱中无用的特征，并筛选出与被测元素定量分析相关的特征进行建模。

本文采用灵敏度分析方法对模型进行特征降维，该算法具体步骤如下：

(1) 利用贝叶斯优化算法搜索得到所有29个特征作为输入的最优模型超参数。

(2) 基于最优超参数和部分样本训练得到SVR模型。

3) 取用步骤2中的所有样本，针对第个i输入特征c ,对样本中特征c的数据分别增大和减少10%后获得样本集e₁和e₂。

4) 利用SVR模型分别预测e₁和e₂得到结果集r₁ 和r₂ ,最后得到特征c的灵敏度S_i =abs(r₁-r₂)。

5) 对所有输入特征重复步骤3和步骤4，最终获得所有特征的灵敏度系数S_i =(1＜=i ＜=29)，对所有的灵敏度系数按从大到小排序得到S^*_i=(1＜=i ＜=29)，最后选择最高的k个特征作为降维后的模型输入，从而提高模型精度，k满足：

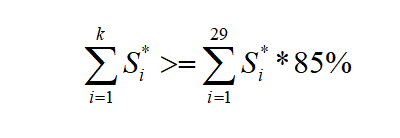
2.3基于BOA-SVR的XRF定量分析策略

最后，基于灵敏度分析和BOA-SVR，本文提出了一种新的XRF元素定量分析策略。针对光谱样本数据，首先利用迭代小波扣除本底，计算各元素组分信息，然后基于灵敏度分析方法计算得到各特征对被测元素的灵敏度，最后从大到小选择灵敏度总和占比高于90%的元素作为输入特征建立模型。算法具体流程如图2所示。

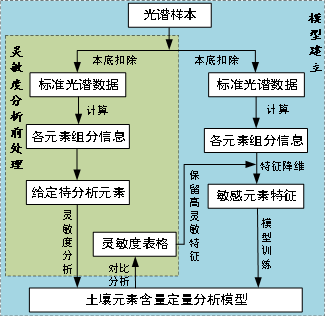
图2 基于BOA-SVR的定量分析算法流程图

3.1基于灵敏度分析的特征降维方法验证

为了筛选出与被测元素定量分析相关的特征建立模型，本文采用了灵敏度分析方法进行特征降维，以As元素为例，基于灵敏度分析后得到测试结果如图3所示。结果表明，29种输入元素的组分信息中Fe、Co、Ti、As、Sb、Ca、Pb对As元素定量分析分析影响最大。上述结果在物理分析中也能得到一定验证，其中As元素的分析受到As元素自身组分信息的影响，但是由于As在土壤中是相对微量的元素，因此影响程度不高。同时，由于As的Kα峰和Pb的Lα峰重叠，因此As也会受到Pb元素的影响，在As中加入Pb可以进一步提高精度。而Fe元素是土壤元素中成分占比最大的元素，远远超过了其它元素，因此Fe的组分信息也是分析中的一个重要输入特征。

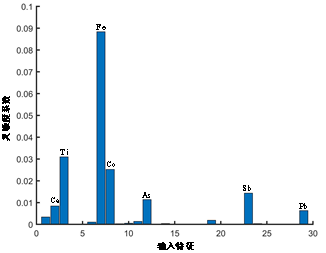
图3 As元素灵敏度分析结果

为了验证特征降维的有效性，在获得了各特征灵敏度排序后依次取前i(1=<i<=29)维最高灵敏度的特征，从一个到完整的29个特征作为输入参数用于模型训练，最后通过基于BOA-SVR的留一交叉验证方法来对比不同特征维度下模型的精度，并以R²_cv和 RMSECV作为评价指标，结果如图4所示。当特征维度较小时(i<5)，即使选择灵敏度最高的维度也无法较好拟合出被测元素，RMSECV值非常高。随着输入特征变多，模型精度逐渐提高，直到特征维度到达7维时模型精度最高，此时RMSECV和R²_cv分别达到最小值和最大值，此时输入特征刚好包含了灵敏度最大的7个特征Fe、Co、Ti、As、Sb、Ca、Pb。随着特征维度的进一步加大，很多与As元素基本不相关的特征引入，反而影响模型的准确性和稳定性，验证了基于灵敏度分析的有效性和特征降维方法的必要性。

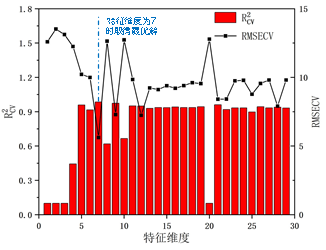
图4 不同特征维度下的实验结果

3.2定量分析方法验证

选择重金属元素Cu和微量重金属元素As作为待测元素对本文算法进行验证。首先对Cu元进行定量分析验证，在验证中，将实验样品分为训练集和测试集两个集合，分别用于外部验证和内部验证。然后，基于灵敏度分析得出Cu元素主要受到Fe、Co、Ni、Cu等组分信息的影响，选择最优输入特征为该4种元素。使用最优输入特征和全部特征作为输入，基于贝叶斯优化算法找到最优模型参数，分别建立了预测土壤样品Cu元素含量的SVR定量预测模型。同时以全部特征作为输入建立了单参数PLS模型，通过5倍交叉验证(CV)选择单参数PLS模型的最优主成分个数为9。基于校准集数据分别建立了三种模型，利用这些模型对13个测试集和42个训练集数据中的Cu元素含量进行预测，结果如图5所示。三种模型在13个测试集样本的详细预测结果和相对误差如表1所示，三种模型的整体性能参数对比如表2所示。

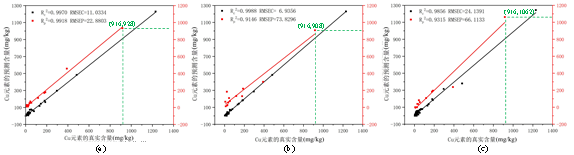
图5 Cu元素的预测结果(a):经过特征降维的SVR模型;(b):全部特征作为输入的SVR模型;(c):PLS模型 

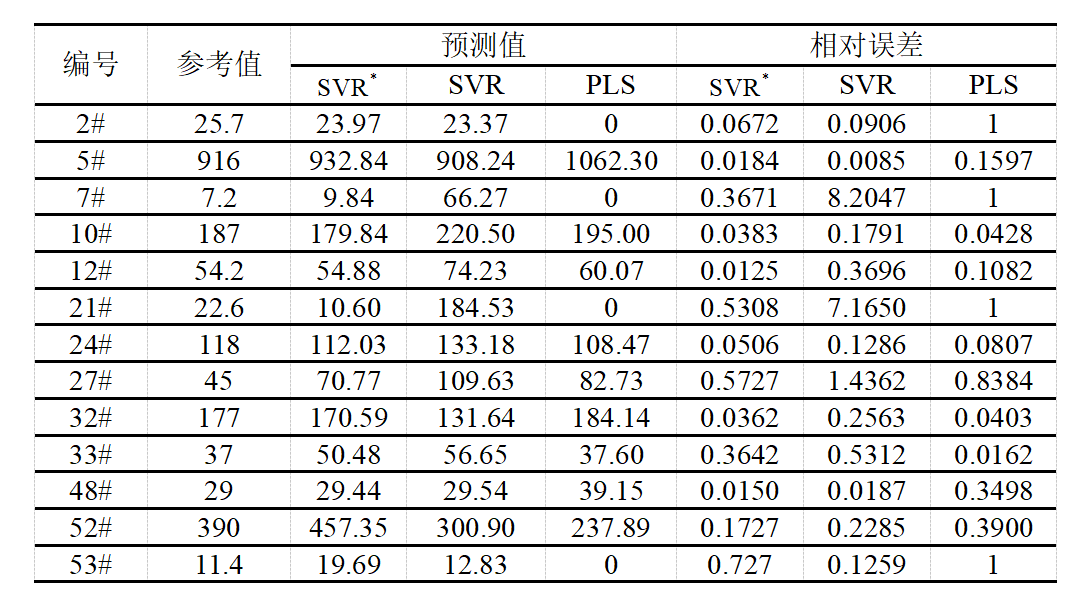
表1 Cu含量预测时三种模型的验证集预测结果，SVR*代表经过特征降维的SVR模型

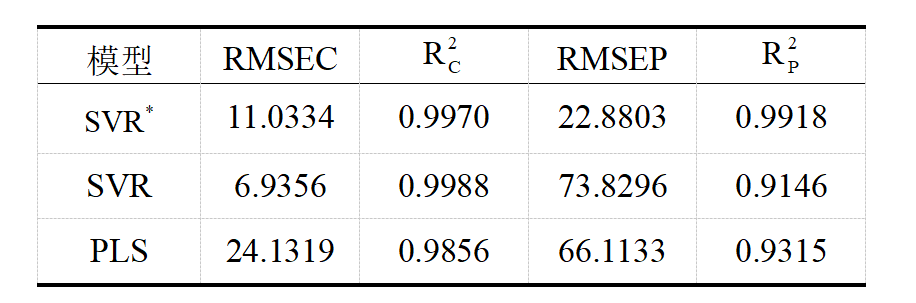
表2 Cu含量预测时三种模型的预测结果对比

对于测试集数据采用全部特征作为输入的SVR模型获得了非常差的结果(R²_p= 0.9146, RMSEP = 73.8296)。由图可以看到真实数据和预测数据的拟合曲线决定系数非常低，说明预测过程随机性较大，同时预测数据和真实数据间误差非常大，精度很差。这表明虽然使用全部输入特征为SVR提供了更多的信息，让模型可以尽可能的拟合训练集数据，但是由于很多特征对于Cu含量的测量是不相关的，并且含有很多噪声信息，这使得模型在预测其它数据时效果很差。因此需要特征降维来筛选出和Cu含量相关的特征，基于4个高灵敏度特征的SVR在预测测试集时获得了非常好的效果(R²_p= 0.9918, RMSEP = 22.8803)，预测数据的一致性较好，拟合曲线的决定系数很高，同时平方根误差RMSEP系数远远低于PLS和全特征SVR模型，表明预测含量基本与实际含量一致。而PLS在测试集的预测中结果也不是很好(R²_p= 0.9315, RMSEP = 66.1133)，虽然在决定系数中表现出一致性较好，但是数据整体表现出偏差，尤其是在元素含量较高的数据上，如图中Cu元素的最高含量为916，但预测结果为1062，偏差非常大，RMSEP指标也表明PLS模型的精度较低。

对As元素做相同的定量分析实验验证，根据灵敏度分析后的结果得到Fe、Co、Ti、As、Sb、Ca、Pb等与As元素测量最相关的7种元素特征。然后基于校准集数据分别建立三种模型，利用这些模型对测试集和训练集数据中的Cu元素含量进行预测，结果如图6所示，三种模型的整体参数对比如表3所示。

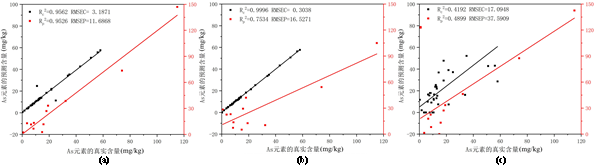
图6 As元素的预测结果(a):经过特征降维的SVR模型;(b):全部特征作为输入的SVR模型;(c):PLS模型 

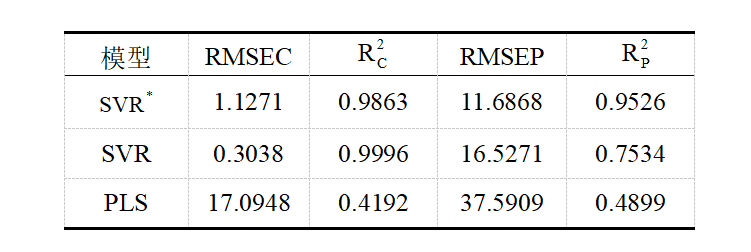
表3 As含量预测时三种模型的预测结果对比

如结果所示，As元素的测量效果比Cu元素的测量效果整体差了不少，这是由于As元素在土壤中含量本身非常微量，导致仪器自身和测量过程中的噪声会对As元素的测量带来较大的影响，影响结果精度，但是在结果的横向对比中也凸显了本文算法的优越性。和Cu元素测量的结论相同，在对训练集数据进行预测时，采用全部特征作为输入的SVR模型也取得了最好的效果，其预测结果和原数据几乎一致(R²_c= 0.9996, RMSEC = 0.3038)，但是模型的训练出现了过拟合的问题，导致在对测试集数据预测时表现非常差(R²_p= 0.7534, RMSEP = 16.5271)，模型泛化能力很弱。而经过灵敏度降维后的SVR模型在三种算法中性能最好，在训练集预测和测试集预测中都获得了相对较好的预测结果(R²_c= 0.9863,RMSEC=1.1271,R²_p=0.9526, RMSEP = 11.6868)。结果表明，基于高灵敏度特征为输入变量构建BOA-SVR定量模型是定量分析土壤中的元素含量的一种可行方法。

本文主要研究了XRF技术结合SVR算法定量分析土壤中各元素含量的可行性。首先，针对XRF光谱样本数据，采用迭代离散小波变换(IDWT)对样本进行预处理，然后计算样本中各元素的组分信息作为模型输入提高预测精度。然后，针对被测元素，基于灵敏度分析方法获得与被测元素测量相关的特征，实现特征降维。最后，基于最优输入变量和BOA-SVR构建最优定量分析模型，将模型应用于土壤中Cu元素和As元素的定量分析。在分析实验中，采用高灵敏度的Fe、Co、Ni、Cu等4个特征作为输入和以Fe、Co、Ti、As、Sb、Ca、Pb等7个特征作为输入的SVR模型分别在定量分析中获得了最好的预测结果。结果表明，基于灵敏度分析的特征降维方法可以剔除掉与被测元素无关的特征和噪声数据，提高模型精度。综上所述，XRF结合BOA-SVR是定量分析土壤元素的一种有效工具。

服务热线|4000-988-166
联系电话|133-7683-5869
联系微信|tecsync_sale

（PS:发送时请备注公司或合作项目哦）